I used to be very afraid of a matrix question. I now view it as a bit of a gift, as it’s a highly visual format, and graphs and trees are a little harder to mentally parse. But the matrix structure has some tricks to it that it simply helps you to know. i.e. Matrix rotation is pretty difficult to write a raw algorithm for but does it help you know that rotation is the same as transposing and then inverting each row? I think that only helps if you know exactly what transposing is. Let’s start there.

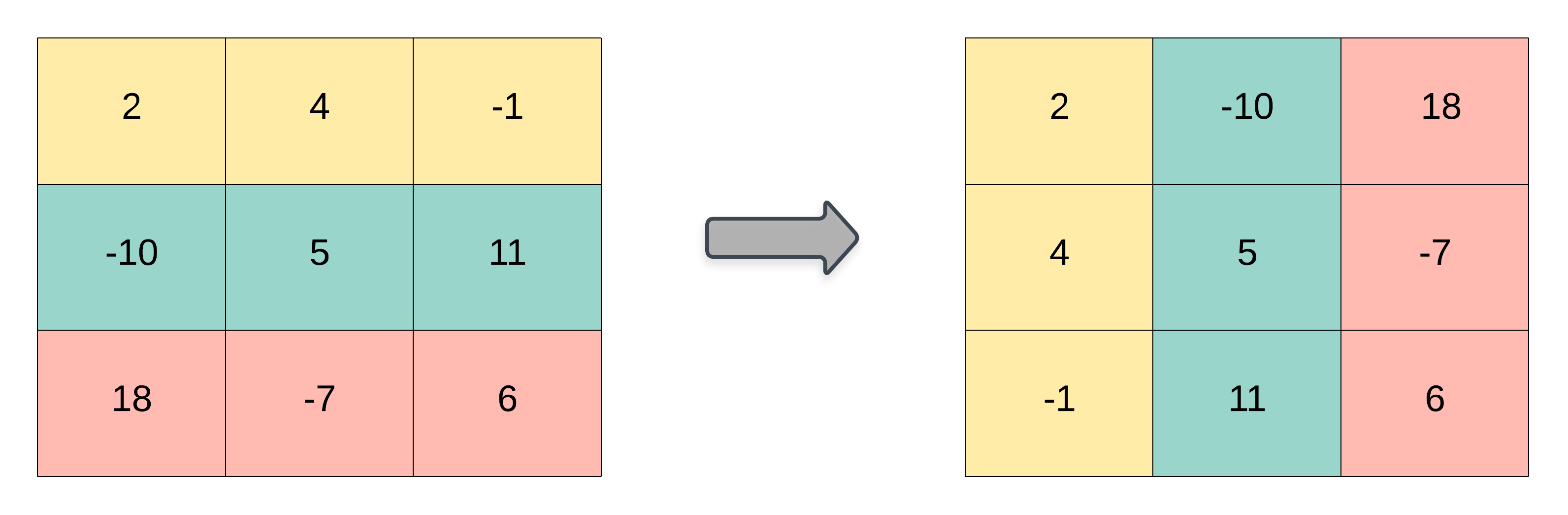
Sometimes you might get a question based only on this. So I have an approach that I’ve learned to help here. This is not the most efficient way to get the matrix transposed but you can pull it out to help with a challenge where algorithmic complexity is a 2nd tier. For this trick, you need to know about *args. From google:

In Python, args is used to allow a function to accept a variable number of positional arguments. These arguments are collected into a tuple, which can be accessed within the function. For example, a function defined as def fun(args): can accept any number of arguments, and they will be stored in the args tuple inside the function.

You can also do this in Javascript with call and apply. For the matrix, this turns

[
['a', 'b', 'c']
['d', 'e', 'f']
['g', 'h', 'i']
]

into

['a', 'b', 'c'] , ['d', 'e', 'f'] , ['g', 'h', 'i']

which then are now eligible to be zipped. Zipping in python:

In Python, the zip() function aggregates elements from multiple iterables (like lists, tuples, or sets) into a single iterable of tuples. Each tuple contains elements from the input iterables at the same index. If the input iterables have different lengths, zip() stops when the shortest iterable is exhausted.

ok so in plain english let’s take the xth item and make a tuple, which is what transposing is of course. The remaining issue is we now have tuples and not lists. That’s were we unfortunately could do something efficient or we could just force what we have to tuples. I’m forcing them for now but I will circle back in a later post.

zip(['a', 'b', 'c'] , ['d', 'e', 'f'] , ['g', 'h', 'i'])

#-->

('a', 'd', 'g') , ('b', 'e', 'h') , ('c', 'f', 'i')

So close but not what we want! Force it to a list (TWICE!) to complete the transpose.

def transpose(matrix):
        return list(list(zip(*matrix)))

Of course this was the only the first half. We wanted to rotate the matrix. So what is inverting? This is hard for me to understand the python shorthand for this but to reverse a string or array in python you just need to get

row = ['a', 'b', 'c'] 
print(row[::-1]) # -> ['c', 'b', 'a']

I personally hate this python syntax, it looks like an emoji and is clearly super hipster. What it means (from Stack Overflow):

list[<start>:<stop>:<step>]

So, when you do a[::-1], it starts from the end towards the first taking each element. So it reverses a. This is applicable for lists/tuples as well.

So with this technique we can skip one of the list steps, it works on tuples. Rotating in place…

def rotate(matrix):
        transpose = list(zip(*matrix))
        for row in range(len(matrix)):
                matrix[x] = transpose[i][::-1]
        return matrix

Most of the other solutions I saw for this involved lots of for loops. Those are probably better for a stronger understanding of brute force manipulation, which will help for sliding window type problems, however, this kind of thinking helps you leverage the matrix’s unique shape to do some tricks. Enjoy!