a king's tour
So I recently got this one at a company I was ok not working at. The interview shows me 2 3 x 3 arrays with numbers 0-9, and a 3rd 3 x 3 array, this one numbered 4-12. The goal with this problem is when given the path of a king on a chessboard, is this a valid route where the king travels through each square on the board sequentially.

Before time expired I was able to put together that this is a recursive problem, that from the starting point the algorigthm would travel to 8 points each recursive round until landing on a value 9 + our starting value: (0, 1, 2 … 7, 8, 9) or (4, 5, 6 … 10, 11, 12)
The much more common problem on the internet is the path of the knight.
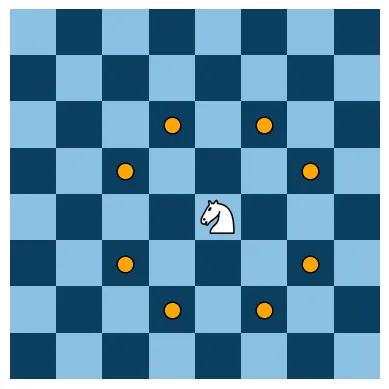
Seeing this image really helped me visualize the legal moves for the knight as coordinate tuples. For Example, the knight is
LEGAL_MOVES: list[tuple(int, int)] =
[(2,1),(-2,1),(2,-1),(-2,-1),(1,2),(-1,2),(1,-2),(-1,-2)]
That’s a different problem! King’s even easier.
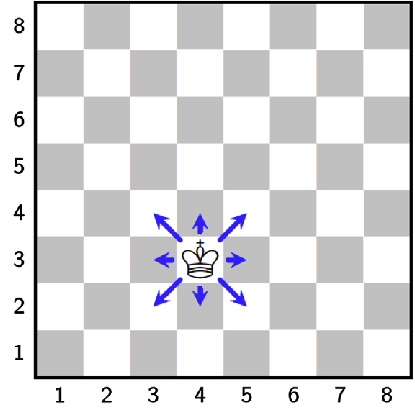
LEGAL_MOVES: list[tuple(int, int)] = [(0, 1),(1, 0),(1, 1),(-1, -1),(0, -1),(-1, 0),(-1, 1),(1, -1)]
During the interview I pursued this as a if / else tree, which is terrible. A better way to do it I found afterwards. This is going to show a structure that confused me initially.
names = ['King', 'Queen', 'Joker']
any(n in 'King and john' for n in names) # -> True
all(n in 'King and Queen' for n in names) # -> False
This structure is another way of saying:
# any(n in 'King and john' for n in names)
for n in names:
if n in 'King and john':
return True
else:
return False
So from this we will take
# any( ~recurse through 8 directions ~ for dx, dy in LEGAL_MOVES)
This psuedocode eventually looks like
any(is_valid(grid, x + dx, y + dy, expected_pos + 1) for dx, dy in LEGAL_MOVES)
So since we know this is recursive, that means is_valid is going to get called many many times. For it to work, is_valid needs many False routes, a continue route each round unless it fails, and one single successful route, i.e. getting to starting_value + n x n (9 in this case)
So we need to start at the starting point. Then we need to travel to each legal move, and then you need to bounce if you are off the board or the next value isn’t exactly n + 1.
# Dead Ends!
if x >= len(grid) or y >= len(grid[0]) or x < 0 or y < 0 or grid[x][y] != expected_pos:
return False
The case for the True case is easy enough, calculate from the board provided (the knight’s case definitely needs like a 5 x 5 or 6 x 6 board)
if expected_pos == len(grid) * len(grid[0]) - 1:
return True
The last piece is understanding all these pieces coming together with the arguments and the recursive call.
def checkValidGrid(grid: list[list[int]], i_x, i_y, starting_val) -> bool:
Let’s try to get it all.
LEGAL_MOVES: list[tuple[int, int]] = [(0, 1),(1, 0),(1, 1),(-1, -1),(0, -1),(-1, 0),(-1, 1),(1, -1)]
def checkValidGrid(grid: list[list[int]], i_x, i_y, starting_val) -> bool:
# Recursive Function
def is_valid(grid: list[list[int]], x: int, y: int, expected_pos: int) -> bool:
# Dead Ends
if x >= len(grid) or y >= len(grid[0]) or x < 0 or y < 0 or grid[x][y] != expected_pos:
return False
# Success
if expected_pos == len(grid) * len(grid[0]) - 1:
return True
# Keep looking. i.e. 0 -> finding 1 -> finding 2, etc...
return any(is_valid(grid, x + dx, y + dy, expected_pos + 1) for dx, dy in LEGAL_MOVES)
# Starting us off!
return is_valid(grid, i_x, i_y, starting_val)
# Test cases
print(checkValidGrid([[3, 2, 1],[6, 4, 0],[5, 7, 8]], 1, 2, 0)) # -> True
print(checkValidGrid([[7, 6, 5],[10, 8, 4],[9, 11, 12]], 1, 2, 4)) # -> True
print(checkValidGrid([[1, 2, 3],[7, 4, 8],[6, 5, 9]], 0, 0, 1)) # -> False
Hit me up if you have any questions. Hopefully this one makes more sense.